如图,在平面直角坐标系中,直线
 分别交
分别交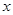 轴、
轴、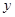 轴于
轴于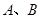 两点.点
两点.点 、
、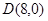 ,以
,以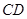 为一边在
为一边在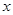 轴上方作矩形
轴上方作矩形 ,且
,且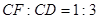 .设矩形CDEF与
.设矩形CDEF与 ABO重叠部分的面积为S.
ABO重叠部分的面积为S. 
(1)求点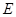 、
、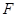 的坐标;
的坐标;
(2)当b值由小到大变化时,求s与b的函数关系式;
(3)若在直线 上存在点
上存在点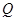 ,使
,使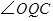 等于
等于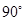 ,请直接写出
,请直接写出 的取值范围.
的取值范围.
相关知识点
推荐套卷
如图,在平面直角坐标系中,直线
 分别交
分别交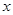 轴、
轴、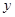 轴于
轴于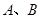 两点.点
两点.点 、
、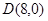 ,以
,以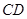 为一边在
为一边在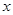 轴上方作矩形
轴上方作矩形 ,且
,且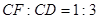 .设矩形CDEF与
.设矩形CDEF与 ABO重叠部分的面积为S.
ABO重叠部分的面积为S. 
(1)求点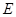 、
、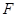 的坐标;
的坐标;
(2)当b值由小到大变化时,求s与b的函数关系式;
(3)若在直线 上存在点
上存在点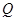 ,使
,使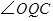 等于
等于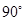 ,请直接写出
,请直接写出 的取值范围.
的取值范围.