从某校参加2012年全国高中数学联赛预赛的450名同学中,随机抽取若干名同学,将他们的成绩制成频率分布表,下面给出了此表中部分数据.
(1)根据表中已知数据,你认为在①、②、③处的数值分别为 , , .
(2)补全在区间 [70,140] 上的频率分布直方图;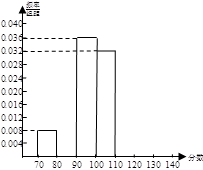
(3)若成绩不低于100分的同学能参加决赛,那么可以估计该校大约有多少学生能参加决赛?
相关知识点
推荐套卷
从某校参加2012年全国高中数学联赛预赛的450名同学中,随机抽取若干名同学,将他们的成绩制成频率分布表,下面给出了此表中部分数据.
(1)根据表中已知数据,你认为在①、②、③处的数值分别为 , , .
(2)补全在区间 [70,140] 上的频率分布直方图;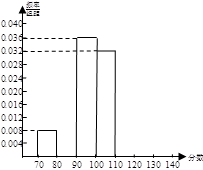
(3)若成绩不低于100分的同学能参加决赛,那么可以估计该校大约有多少学生能参加决赛?