（本小题满分13分）
已知抛物线、椭圆和双曲线都经过点
，它们在
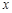轴上有共同焦点，椭圆和双曲线的对称轴是坐标轴，抛物线的顶点为坐标原点．
（1）求这三条曲线的方程；
（2）对于抛物线上任意一点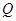
，点
都满足
，求
的取值范围．
相关试题
中，已知
，
中，
、
、
所对的边分别为
、
、
，
，
，
，求
的值。
中，若
，
，求：
的值。推荐套卷
（本小题满分13分）
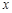已知抛物线、椭圆和双曲线都经过点，它们在轴上有共同焦点，椭圆和双曲线的对称轴是坐标轴，抛物线的顶点为坐标原点．
（1）求这三条曲线的方程；
（2）对于抛物线上任意一点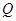，点都满足，求的取值范围．
粤公网安备 44130202000953号