(本题满分12分)在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日至30日,评委会把同学们上交作品的件数按照5天一组分组统计,绘制了频率分布直方图(如图所示).已知从左到右各长方形的高的比为2:3:4:6:4:1,第三组的频数为12,请解答下列各题.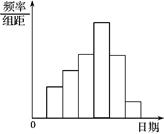
(1)本次活动共有多少件作品参加评比?
(2)哪组上交的作品数量最多?有多少件?
(3)经过评比,第四组和第六组分别有10件、2件作品获奖,问这两组哪一组获奖率较高?
相关知识点
推荐套卷
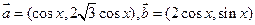 ,且
,且
 的最小正周期及单调递增区间。
的最小正周期及单调递增区间。 成立,
成立,

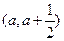 上存在极值,其中a >0,求实数a的取值范围;
上存在极值,其中a >0,求实数a的取值范围;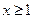 时,不等式
时,不等式 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;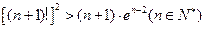 。
。 :
: 的焦点为
的焦点为
 ,过点
,过点 交抛物线
交抛物线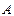 、
、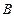 两点;椭圆
两点;椭圆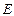 的中心在原点,焦点在
的中心在原点,焦点在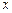 轴上,点
轴上,点 .
. 、
、 ,切线
,切线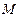 .证明:
.证明: ;
;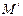 ,经过点
,经过点 、
、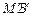 (
( 、
、 为切点),使得直线
为切点),使得直线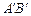 过点
过点 中,已知
中,已知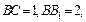
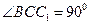 ,
, 侧面
侧面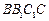

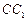 (不包含端点
(不包含端点 上确定一点
上确定一点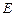 的位置,使得
的位置,使得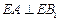 (要求说明理由).
(要求说明理由).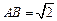 ,求二面角
,求二面角 的大小.
的大小.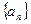 中,
中,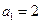 ,
,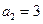 ,其前
,其前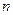 项和
项和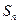 满足
满足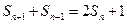 (
(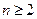 ,
,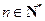
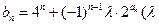 为非零整数,
为非零整数,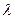 的值,使得对任意
的值,使得对任意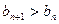 成立.
成立. 粤公网安备 44130202000953号
粤公网安备 44130202000953号