(本小题满分12分)
过抛物线焦点垂直于对称轴的弦叫做抛物线的通径。如图,已知抛物线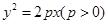 ,过其焦点F的直线交抛物线于
,过其焦点F的直线交抛物线于 、
、 两点。过
两点。过 、
、 作准线的垂线,垂足分别为
作准线的垂线,垂足分别为 、
、 .
.
(1)求出抛物线的通径,证明 和
和 都是定值,并求出这个定值;
都是定值,并求出这个定值;
(2)证明:  .
.
推荐套卷
(本小题满分12分)
过抛物线焦点垂直于对称轴的弦叫做抛物线的通径。如图,已知抛物线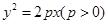 ,过其焦点F的直线交抛物线于
,过其焦点F的直线交抛物线于 、
、 两点。过
两点。过 、
、 作准线的垂线,垂足分别为
作准线的垂线,垂足分别为 、
、 .
.
(1)求出抛物线的通径,证明 和
和 都是定值,并求出这个定值;
都是定值,并求出这个定值;
(2)证明:  .
.