(本小题满分12分)
设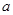
∈R，函数
=
（
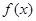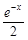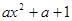），其中e是自然对数的底数．
（1）判断f (x)在R上的单调性；
（2）当– 1 <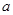< 0时，求f (x)在[1，2]上的最小值．
选做题：请考生从给出的3道题中任选一题做答，并在答题卡上把所选题目的题号用2B铅笔涂黑．注意所做题目的题号必须与所涂的题号一致，在答题卡选答区域指定位置答题．如果多做，则按所做的第一题计分．
相关试题
=" x" +
,
为常数，且
是奇函数且在区间
上是减函数.
的奇偶性；
上是增函数还是减函数？并证明之.
且q是假命题，求c的取值范围。
的定义域为集合M，函数
的定义域为集合N．
，
．
.相关知识点
推荐套卷
(本小题满分12分)
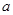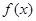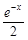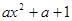设∈R，函数 =（），其中e是自然对数的底数．
（1）判断f (x)在R上的单调性；
（2）当– 1 <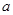< 0时，求f (x)在[1，2]上的最小值．
选做题：请考生从给出的3道题中任选一题做答，并在答题卡上把所选题目的题号用2B铅笔涂黑．注意所做题目的题号必须与所涂的题号一致，在答题卡选答区域指定位置答题．如果多做，则按所做的第一题计分．
粤公网安备 44130202000953号