为迎接建党90周年,某班开展了一次“党史知识竞赛”,竞赛分初赛和决赛两个阶段进行,在初赛后,把成绩(满分为100分,分数均为整数)进行统计,制成如图频率分布表:
(1)求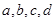 的值;
的值;
(2)决赛规则如下:为每位参加决赛的选手准备四道题目,选手对其依次作答,答对两道就终止答题,并获得一等奖,若题目答完仍然只答对一道,则获得二等奖.某同学进入决赛,每道题答对的概率P的值恰好与频率分布表中不少于90分的频率的值相同.设该同学决赛中答题个数为X,求X的分布列以及X的数学期望.
推荐套卷
为迎接建党90周年,某班开展了一次“党史知识竞赛”,竞赛分初赛和决赛两个阶段进行,在初赛后,把成绩(满分为100分,分数均为整数)进行统计,制成如图频率分布表:
(1)求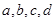 的值;
的值;
(2)决赛规则如下:为每位参加决赛的选手准备四道题目,选手对其依次作答,答对两道就终止答题,并获得一等奖,若题目答完仍然只答对一道,则获得二等奖.某同学进入决赛,每道题答对的概率P的值恰好与频率分布表中不少于90分的频率的值相同.设该同学决赛中答题个数为X,求X的分布列以及X的数学期望.