(本题满分16分,第1小题4分,第2小题6分,第3小题6分)
设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1、F2,线段OF1、OF2的中点分别为B1、B2,且△AB1B2是面积为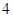 的直角三角形.过B1作直线l交椭圆于P、Q两点.
的直角三角形.过B1作直线l交椭圆于P、Q两点.
(1) 求该椭圆的标准方程;
(2) 若 ,求直线l的方程;
,求直线l的方程;
(3) 设直线l与圆O:x2+y2=8相交于M、N两点,令|MN|的长度为t,若t∈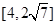 ,求△B2PQ的面积
,求△B2PQ的面积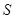 的取值范围.
的取值范围.
相关知识点
推荐套卷
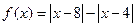 .
.
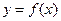 的图像.
的图像.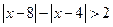 .
.
 中都有5个标有数字1,3个标有数字2,2个标有数字3。两人同时分别从自己的小球中任意抽取1个,规定:若抽取的两个小球上的数字相同,则甲获胜,否则乙获胜,求乙获胜的概率。
中都有5个标有数字1,3个标有数字2,2个标有数字3。两人同时分别从自己的小球中任意抽取1个,规定:若抽取的两个小球上的数字相同,则甲获胜,否则乙获胜,求乙获胜的概率。 2)这个两位数是偶数的概率;
2)这个两位数是偶数的概率; 粤公网安备 44130202000953号
粤公网安备 44130202000953号