（本小题满分
分）设函数
的最高点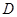
的坐标为（
），由最高点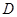运动到相邻最低点时，函数图形与
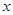的交点的坐标为（
）.
（1）求函数
的解析式.
（2）当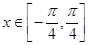
时，求函数的最大值和最小值以及分别取得最大值和最小值时
相应的自变量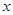的值.
（3）将函数
的图象向右平移
个单位，得到函数
的图象，求函数的单调减区间.
中，
，
。
，求数列
的前
项和
的解集为
,求实数
的取值范围。
首项为
，公比为q,求（1）该数列的前n项和
。
不是等比数列
中，已知
，
，试判断推荐套卷
（本小题满分分）设函数的最高点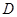的坐标为（），由最高点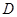运动到相邻最低点时，函数图形与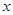的交点的坐标为（）.
（1）求函数的解析式.
（2）当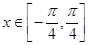时，求函数的最大值和最小值以及分别取得最大值和最小值时
相应的自变量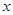的值.
（3）将函数的图象向右平移个单位，得到函数的图象，求函数的单调减区间.
粤公网安备 44130202000953号