如图的小方格都是边长为1个单位的正方形,按照下列要求作图.(不写作法,只作出图形即可)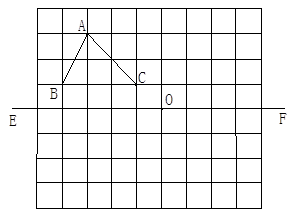
(1)作△ABC关于直线EF的轴对称图形;
(2)将△ABC向右平移4个单位;
(3)作△ABC关于点O的中心对称图形.
相关知识点
推荐套卷
如图的小方格都是边长为1个单位的正方形,按照下列要求作图.(不写作法,只作出图形即可)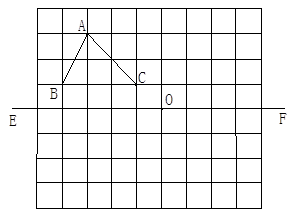
(1)作△ABC关于直线EF的轴对称图形;
(2)将△ABC向右平移4个单位;
(3)作△ABC关于点O的中心对称图形.