(本小题满分12分)为了参加 年贵州省高中篮球比赛,某中学决定从四个篮球较强的班级中选出
年贵州省高中篮球比赛,某中学决定从四个篮球较强的班级中选出 人组成男子篮球队代表所在地区参赛,队员来源人数如下表:
人组成男子篮球队代表所在地区参赛,队员来源人数如下表:
| 班级 |
高三( )班 )班 |
高三( )班 )班 |
高二( )班 )班 |
高二( )班 )班 |
| 人数 |
 |
 |
 |
 |
(I)从这 名队员中随机选出两名,求两人来自同一班级的概率;(II)该中学篮球队经过奋力拼搏获得冠军.若要求选出两位队员代表冠军队发言,设其中来自高三(7)班的人数为
名队员中随机选出两名,求两人来自同一班级的概率;(II)该中学篮球队经过奋力拼搏获得冠军.若要求选出两位队员代表冠军队发言,设其中来自高三(7)班的人数为 ,求随机变量
,求随机变量 的分布列及数学期望
的分布列及数学期望 .
.
推荐套卷
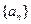 中,
中, 且满足
且满足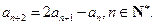
 求
求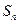 的解析式;
的解析式;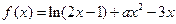 在
在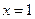 处取得极值.
处取得极值.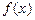 的单调区间;
的单调区间;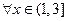 ,
,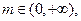
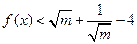 .
.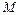 是
是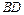 的中点.侧视图是直角梯形,俯视图是等腰直角
的中点.侧视图是直角梯形,俯视图是等腰直角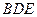 ?若存在,确定点N的位置;
?若存在,确定点N的位置;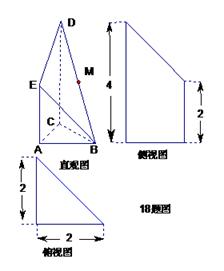
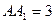 ,俯视图中
,俯视图中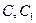 分别是所在边的中点,设
分别是所在边的中点,设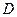 为
为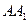 的中点.
的中点.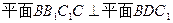 ;
;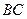 边上是否存在点
边上是否存在点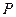 ,使
,使 ?若不存在,说明理由;若存在,请证明你的结论.
?若不存在,说明理由;若存在,请证明你的结论.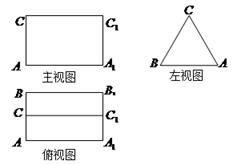
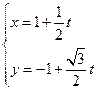 被圆
被圆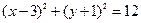 所截得的弦长。
所截得的弦长。 粤公网安备 44130202000953号
粤公网安备 44130202000953号