(满分12分)已知点 ,直线
,直线 :
: 交
交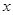 轴于点
轴于点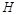 ,点
,点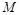 是
是 上的动点,过点
上的动点,过点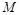 垂直于
垂直于 的直线与线段
的直线与线段 的垂直平分线交于点
的垂直平分线交于点 .
.
(Ⅰ)求点 的轨迹
的轨迹 的方程;(Ⅱ)若 A、B为轨迹
的方程;(Ⅱ)若 A、B为轨迹 上的两个动点,且
上的两个动点,且 证明直线AB必过一定点,并求出该定点.
证明直线AB必过一定点,并求出该定点.
相关知识点
推荐套卷
(满分12分)已知点 ,直线
,直线 :
: 交
交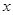 轴于点
轴于点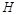 ,点
,点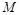 是
是 上的动点,过点
上的动点,过点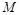 垂直于
垂直于 的直线与线段
的直线与线段 的垂直平分线交于点
的垂直平分线交于点 .
.
(Ⅰ)求点 的轨迹
的轨迹 的方程;(Ⅱ)若 A、B为轨迹
的方程;(Ⅱ)若 A、B为轨迹 上的两个动点,且
上的两个动点,且 证明直线AB必过一定点,并求出该定点.
证明直线AB必过一定点,并求出该定点.