(本小题满分12分)
设定义在区间 上的函数
上的函数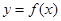 的图象为
的图象为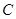 ,
,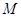 是
是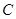 上的任意一点,
上的任意一点,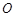 为坐标原点,设向量
为坐标原点,设向量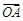 =
= ,
,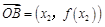 ,
,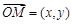 ,当实数λ满足x="λ" x1+(1-λ) x2时,记向量
,当实数λ满足x="λ" x1+(1-λ) x2时,记向量 =λ
=λ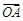 +(1-λ)
+(1-λ) .定义“函数
.定义“函数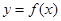 在区间
在区间 上可在标准
上可在标准 下线性近似”是指 “
下线性近似”是指 “
 恒成立”,其中
恒成立”,其中 是一个确定的正数.
是一个确定的正数.
(1)求证: 三点共线;
三点共线;
(2)设函数 在区间[0,1]上可在标准
在区间[0,1]上可在标准 下线性近似,求
下线性近似,求 的取值范围;
的取值范围;
(3)求证:函数 在区间
在区间 上可在标准
上可在标准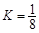 下线性近似.
下线性近似.
(参考数据: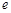 =2.718,
=2.718, )
)
推荐套卷
(本小题满分12分)
设定义在区间 上的函数
上的函数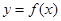 的图象为
的图象为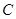 ,
,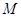 是
是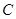 上的任意一点,
上的任意一点,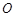 为坐标原点,设向量
为坐标原点,设向量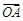 =
= ,
,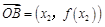 ,
,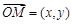 ,当实数λ满足x="λ" x1+(1-λ) x2时,记向量
,当实数λ满足x="λ" x1+(1-λ) x2时,记向量 =λ
=λ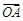 +(1-λ)
+(1-λ) .定义“函数
.定义“函数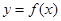 在区间
在区间 上可在标准
上可在标准 下线性近似”是指 “
下线性近似”是指 “
 恒成立”,其中
恒成立”,其中 是一个确定的正数.
是一个确定的正数.
(1)求证: 三点共线;
三点共线;
(2)设函数 在区间[0,1]上可在标准
在区间[0,1]上可在标准 下线性近似,求
下线性近似,求 的取值范围;
的取值范围;
(3)求证:函数 在区间
在区间 上可在标准
上可在标准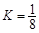 下线性近似.
下线性近似.
(参考数据: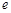 =2.718,
=2.718, )
)