2013年某工厂生产某种产品,每日的成本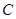 (单位:万元)与日产量
(单位:万元)与日产量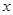 (单位:吨)满足函数关系式
(单位:吨)满足函数关系式 ,每日的销售额
,每日的销售额 (单位:万元)与日产量
(单位:万元)与日产量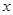 的函数关系式
的函数关系式
已知每日的利润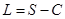 ,且当
,且当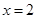 时,
时,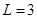 .
.
(1)求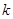 的值;
的值;
(2)当日产量为多少吨时,每日的利润可以达到最大,并求出最大值.
推荐套卷
2013年某工厂生产某种产品,每日的成本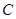 (单位:万元)与日产量
(单位:万元)与日产量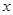 (单位:吨)满足函数关系式
(单位:吨)满足函数关系式 ,每日的销售额
,每日的销售额 (单位:万元)与日产量
(单位:万元)与日产量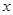 的函数关系式
的函数关系式
已知每日的利润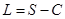 ,且当
,且当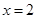 时,
时,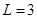 .
.
(1)求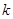 的值;
的值;
(2)当日产量为多少吨时,每日的利润可以达到最大,并求出最大值.