(本小题满分12分)
已知数列{an}的前n项和为Sn，点
在直线
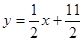上.数列{bn}满足
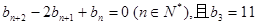，前9项和为153.
（Ⅰ）求数列{an}、{bn}的通项公式；
（Ⅱ）设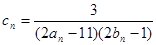
，数列{cn}的前n和为Tn，求使不等式
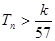对一切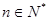
都成立的最大正整数k的值.
x＋1的倾斜角的
，且分别满足下列条件的直线方程：(1)经过点(
，1＋
为空间四边形
的边
上的点，且
，求证：
.
中
，
面
，
，
面
.
相关知识点
推荐套卷
(本小题满分12分)
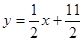已知数列{an}的前n项和为Sn，点在直线上.数列{bn}满足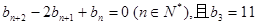，前9项和为153.
（Ⅰ）求数列{an}、{bn}的通项公式；
（Ⅱ）设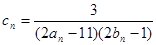，数列{cn}的前n和为Tn，求使不等式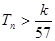对一切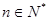都成立的最大正整数k的值.
粤公网安备 44130202000953号