比较下面每小题中两个算式结果的大小(在横线上填“>”、“<”或“=”).
(1)32+42 2×3×4;(2)22+22 2×2×2;(3)12+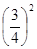 2×1×
2×1×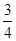 ;
;
(4)(-2) 2+52 2×(-2)×5;(5)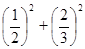
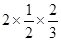 .
.
通过观察上面的算式,请你用字母来表示上面算式中反映的一般规律.
比较下面每小题中两个算式结果的大小(在横线上填“>”、“<”或“=”).
(1)32+42 2×3×4;(2)22+22 2×2×2;(3)12+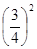 2×1×
2×1×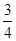 ;
;
(4)(-2) 2+52 2×(-2)×5;(5)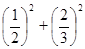
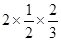 .
.
通过观察上面的算式,请你用字母来表示上面算式中反映的一般规律.