如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.以点O为原点、竖直和水平方向所在的直线为坐标轴、网格边长为单位长,建立平面直角坐标系.设该圆弧所在圆的圆心为点D,连结AD、CD.
请完成下列问题:
(1)出点D的坐标:D___________;
(2)D的半径=_____(结果保留根号);
(3)若扇形DAC是一个圆锥的侧面展开图,则该圆锥的底面面积为__________(结果保留π);
(4)若E(7,0),试判断直线EC与⊙D的位置关系并说明你的理由.
相关知识点
推荐套卷
 。
。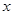 取何值时,
取何值时, 随
随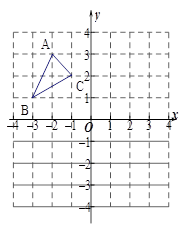

 粤公网安备 44130202000953号
粤公网安备 44130202000953号