如图,已知:椭圆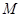 的中心为
的中心为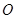 ,长轴的两个端点为
,长轴的两个端点为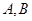 ,右焦点为
,右焦点为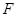 ,
,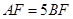 .若椭圆
.若椭圆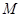 经过点
经过点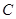 ,
,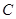 在
在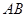 上的射影为
上的射影为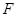 ,且△
,且△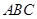 的面积为5.
的面积为5.
(Ⅰ)求椭圆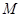 的方程;
的方程;
(Ⅱ)已知圆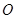 :
: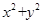 =1,直线
=1,直线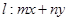 =1,试证明:当点
=1,试证明:当点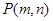 在椭圆
在椭圆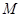 上
上
运动时,直线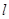 与圆
与圆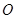 恒相交;并求直线
恒相交;并求直线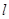 被圆
被圆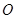 截得的弦长的取值范围.
截得的弦长的取值范围. 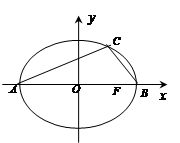
推荐套卷
如图,已知:椭圆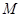 的中心为
的中心为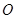 ,长轴的两个端点为
,长轴的两个端点为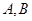 ,右焦点为
,右焦点为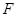 ,
,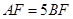 .若椭圆
.若椭圆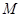 经过点
经过点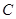 ,
,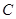 在
在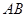 上的射影为
上的射影为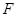 ,且△
,且△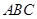 的面积为5.
的面积为5.
(Ⅰ)求椭圆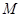 的方程;
的方程;
(Ⅱ)已知圆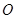 :
: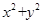 =1,直线
=1,直线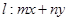 =1,试证明:当点
=1,试证明:当点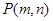 在椭圆
在椭圆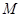 上
上
运动时,直线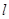 与圆
与圆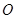 恒相交;并求直线
恒相交;并求直线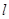 被圆
被圆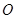 截得的弦长的取值范围.
截得的弦长的取值范围. 