已知点A（2，8），B（x1，y1），C（x2，y2）在抛物线y2=2px上，△ABC的重心与此抛物线的焦点F重合（如图）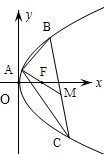
（1）写出该抛物线的方程和焦点F的坐标；
（2）求线段BC中点M的坐标
（3）求BC所在直线的方程．
相关试题
的前n项和
（其中
为常数）,且
="4" 
=8
.
；
的前
项和
.
=
的部分图象如图所示。
=
－
的单调递增区间。
、
、
分别为
三个内角
、
、
的对边，
.
，求
的前
项和
,满足
,
.
的前
；
，证明：
．推荐套卷
已知点A（2，8），B（x1，y1），C（x2，y2）在抛物线y2=2px上，△ABC的重心与此抛物线的焦点F重合（如图）
（1）写出该抛物线的方程和焦点F的坐标；
（2）求线段BC中点M的坐标
（3）求BC所在直线的方程．
粤公网安备 44130202000953号