如图1所示，已知在△ABC和△DEF中， 
，
.
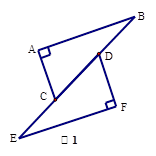
(1)试说明：△ABC≌△FED的理由；
(2)若图形经过平移和旋转后得到如图2，若
,试求∠DHB的度数；
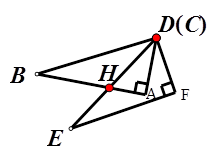
(3）若将△ABC继续绕点D旋转后得到图3，此时D、B、F三点在同一条直线上，若DF:FB=3:2，连结EB，已知△ABD的周长是12，且AB-AD=1，你能求出四边形ABED的面积吗？若能，请求出来；若不能，请说明理由。
相关试题
某城市大剧院地面的一部分为扇形，观众席的座位按下列方式设置：
| 排数 |
1 |
2 |
3 |
4 |
| 座位数 |
50 |
53 |
56 |
59 |
按这种方式排下去，
（1）第5、6排各有多少个座位？
（2）第n排有多少个座位？
（3）根据（2）的代数式，判断第25排有多少个座位？
小虫从某点O出发在一直线上来回爬行，假定向右爬行的路程记为正，向左爬行的路程记为负，爬过的路程依次为（单位：厘米）：
+4，－3， +10，－8， －5， +12，－10
问：（1）小虫是否回到原点O ？
（2）小虫离开出发点O最远是多少厘米？
（3）在爬行过程中，如果每爬行1厘米奖励一粒芝麻，则小虫共可得到多少粒芝麻？
，其中
的值．
（2）
相关知识点
推荐套卷
粤公网安备 44130202000953号