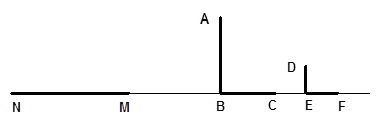如下图,路灯下,一墙墩(用线段AB表示)的影子是BC,小明(用线段DE表示)的影子是EF,在M处有一颗大树,它的影子是MN.
(1)试确定路灯的位置(用点P表示);
(2)在图中画出表示大树高的线段;
(3)若小明的眼睛近似地看成是点D,试画图分析小明能否看见大树。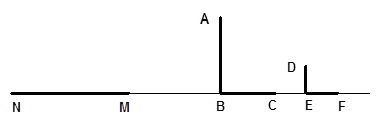
相关知识点
推荐套卷
如下图,路灯下,一墙墩(用线段AB表示)的影子是BC,小明(用线段DE表示)的影子是EF,在M处有一颗大树,它的影子是MN.
(1)试确定路灯的位置(用点P表示);
(2)在图中画出表示大树高的线段;
(3)若小明的眼睛近似地看成是点D,试画图分析小明能否看见大树。