（本小题满分13分）
已知直线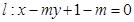
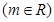，圆
.
(Ⅰ)证明：对任意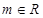
，直线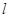
恒过一定点N，且直线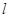与圆C恒有两个公共点；
(Ⅱ)设以CN为直径的圆为圆D（D为CN中点），求证圆D的方程为：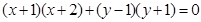
（Ⅲ）设直线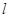与圆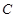
的交于A、B两点，与圆D: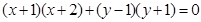交于点
（异于C、N），当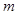
变化时，求证为AB的中点.
相关试题
的定义域为集合
，又
，求
的取值范围；
，当
时，求
及
．
；
．
前
项和为
，满足
．
求数列
的前
;
对任意的
恒成立，求实数
的取值范围．
，
，
时，求
的最小值；
时，求
的最小值。
、
、
，求：推荐套卷
（本小题满分13分）
已知直线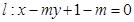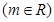，圆.
(Ⅰ)证明：对任意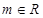，直线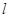恒过一定点N，且直线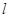与圆C恒有两个公共点；
(Ⅱ)设以CN为直径的圆为圆D（D为CN中点），求证圆D的方程为：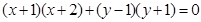
（Ⅲ）设直线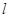与圆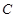的交于A、B两点，与圆D: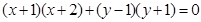交于点（异于C、N），当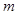变化时，求证为AB的中点.
粤公网安备 44130202000953号