(本题满分12分,第(Ⅰ)问6分,第(Ⅱ)问6分)如图一,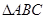 是正三角形,
是正三角形,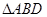 是等腰直角三角形,
是等腰直角三角形,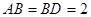 .将
.将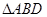 沿
沿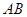 折起,使得
折起,使得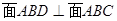 , 如图二,
, 如图二,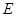 为
为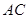 的中点
的中点
(Ⅰ)求证: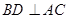 ;
;
(Ⅱ)求 的面积;
的面积;
(Ⅲ)求三棱锥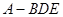 的体积.
的体积.
相关知识点
推荐套卷
(本题满分12分,第(Ⅰ)问6分,第(Ⅱ)问6分)如图一,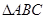 是正三角形,
是正三角形,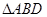 是等腰直角三角形,
是等腰直角三角形,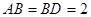 .将
.将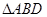 沿
沿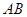 折起,使得
折起,使得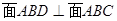 , 如图二,
, 如图二,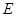 为
为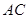 的中点
的中点
(Ⅰ)求证: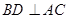 ;
;
(Ⅱ)求 的面积;
的面积;
(Ⅲ)求三棱锥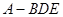 的体积.
的体积.