如图,某观测站 在城
在城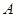 的南偏西
的南偏西 的方向上,由
的方向上,由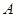 城出发有一公路,走向是南偏东
城出发有一公路,走向是南偏东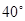 ,在
,在 处测得距
处测得距 为31公里的公路上
为31公里的公路上 处,有一人正沿公路向
处,有一人正沿公路向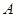 城走去,走了20公里后,到达
城走去,走了20公里后,到达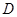 处,此时
处,此时 、
、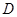 间距离为
间距离为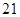 公里,问此人还需要走多少公里到达
公里,问此人还需要走多少公里到达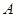 城.
城.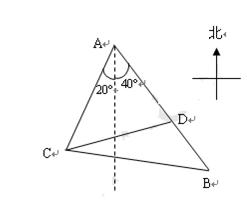
推荐套卷
如图,某观测站 在城
在城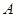 的南偏西
的南偏西 的方向上,由
的方向上,由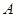 城出发有一公路,走向是南偏东
城出发有一公路,走向是南偏东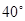 ,在
,在 处测得距
处测得距 为31公里的公路上
为31公里的公路上 处,有一人正沿公路向
处,有一人正沿公路向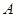 城走去,走了20公里后,到达
城走去,走了20公里后,到达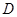 处,此时
处,此时 、
、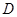 间距离为
间距离为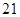 公里,问此人还需要走多少公里到达
公里,问此人还需要走多少公里到达 城.
城.