如图,在平面直角坐标系中,抛物线y=-x2+bx+c与y轴交于点A(0,3),且经过点(5,-2),点B与点A关于对称轴对称,过点B作BC⊥x轴,垂足为C,连结OB.
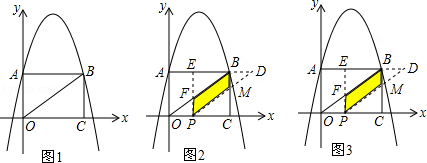
(1)求二次函数的解析式,并求出点B的坐标.
(2)把△AOB以每秒1个单位的速度向右平移,得到△PDE,PE交OB于点F,PD交BC于点M,设向右平移运动的时间为t(s).设平移过程中与△OBC重叠部分的面积为S,试探求S 与t的函数关系式,并求当t为何值时,S最大?
(3)在(2)的条件下,是否存在某一时刻t,使△OCE为等腰三角形?若存在,求出t;若不存在,请说明理由.