网格中有一个小甲虫（
），它喜欢吃牛粪，它又会把吃剩的牛粪滚成牛粪球（
）藏进仓库（
）.规定向左为L，向右为R，向上为U，向下D，如：L1表示向左平移一格，D2表示向下平移2格.例如：要把左图中的所有的牛粪球推到最近的仓库里，可以编写程序：L1-R1-U2-D3-R2-U1，小甲虫就能把所有的牛粪球推到最近的仓库.你来试一试，可编写一个怎样的程序才能使小甲虫把右边图上的所有牛粪球推到最近的仓库里.（只需写出一种可行的程序即可）
相关试题
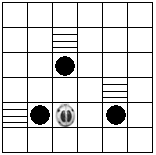
网格中有一个小甲虫（），它喜欢吃牛粪，它又会把吃剩的牛粪滚成牛粪球（）藏进仓库（）.规定向左为L，向右为R，向上为U，向下D，如：L1表示向左平移一格，D2表示向下平移2格.例如：要把左图中的所有的牛粪球推到最近的仓库里，可以编写程序：L1-R1-U2-D3-R2-U1，小甲虫就能把所有的牛粪球推到最近的仓库.你来试一试，可编写一个怎样的程序才能使小甲虫把右边图上的所有牛粪球推到最近的仓库里.（只需写出一种可行的程序即可）
和点
，给出如下定义：若
，则称点
为点
的限变点．例如：点
的限变点的坐标是
的限变点的坐标是
．
的限变点的坐标是___________；
，
中有一个点是函数
图象上某一个点的限变点，这个点是_______________；
的图象上，其限变点
的取值范围是
，求
的取值范围；
的二次函数
的图象上，其限变点
或
，其中
．令
，求
关于
的函数解析式及
粤公网安备 44130202000953号