两个反比例函数 和
和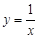 在第一象限内的图象如图所示,点P在
在第一象限内的图象如图所示,点P在 的图象上,PC⊥x轴于点C,交
的图象上,PC⊥x轴于点C,交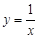 的图象于点A,PD⊥y轴于点D,交
的图象于点A,PD⊥y轴于点D,交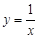 的图象于点B,当点P在
的图象于点B,当点P在 的图象上运动时,以下结论:
的图象上运动时,以下结论:
①△ODB与△OCA的面积相等;
②四边形PAOB的面积不会发生变化;
③PA与PB始终相等;
④当点A是PC的中点时,点B一定是PD的中点.
其中一定正确的结论有哪几个?对正确的结论要说明理由!
两个反比例函数 和
和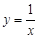 在第一象限内的图象如图所示,点P在
在第一象限内的图象如图所示,点P在 的图象上,PC⊥x轴于点C,交
的图象上,PC⊥x轴于点C,交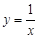 的图象于点A,PD⊥y轴于点D,交
的图象于点A,PD⊥y轴于点D,交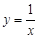 的图象于点B,当点P在
的图象于点B,当点P在 的图象上运动时,以下结论:
的图象上运动时,以下结论:
①△ODB与△OCA的面积相等;
②四边形PAOB的面积不会发生变化;
③PA与PB始终相等;
④当点A是PC的中点时,点B一定是PD的中点.
其中一定正确的结论有哪几个?对正确的结论要说明理由!