抛物线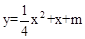
的顶点在直线
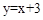上，过点F（－2，2）的直线交该抛物线于点M、N两点（点M在点N的左边），MA⊥x轴于点A，NB⊥x轴于点B．
（1）(3分)先通过配方求抛物线的顶点坐标（坐标可用含m的代数式表示），再求m的值；
（2）(3分)设点N的横坐标为a，试用含a的代数式表示点N的纵坐标，并说明NF＝NB；
（3）(3分)若射线NM交x轴于点P，且PA×PB＝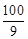
，求点M的坐标．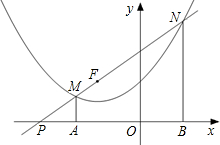
相关试题
，其中x=3,y=1
；
．相关知识点
推荐套卷
抛物线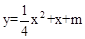的顶点在直线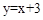上，过点F（－2，2）的直线交该抛物线于点M、N两点（点M在点N的左边），MA⊥x轴于点A，NB⊥x轴于点B．
（1）(3分)先通过配方求抛物线的顶点坐标（坐标可用含m的代数式表示），再求m的值；
（2）(3分)设点N的横坐标为a，试用含a的代数式表示点N的纵坐标，并说明NF＝NB；
（3）(3分)若射线NM交x轴于点P，且PA×PB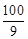＝，求点M的坐标．
粤公网安备 44130202000953号