某工厂有一段旧墙长14m,现准备利用这段旧墙为一面建造平面图形为矩形,面积为126m2的厂房,工程条件是:
(1) 建1m新墙的费用为a元;(2) 修1m旧墙的费用为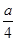 元;(3) 拆去1m的旧墙,用可得的建材建1m的新墙的费用为
元;(3) 拆去1m的旧墙,用可得的建材建1m的新墙的费用为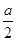 元,经讨论有两种方案:
元,经讨论有两种方案:
①利用旧墙一段x m(0<x<14)为矩形一边;
②矩形厂房利用旧墙的一面边长x≥14,问如何利用旧墙建墙费用最省?
试比较①②两种方案哪个更好。
推荐套卷
某工厂有一段旧墙长14m,现准备利用这段旧墙为一面建造平面图形为矩形,面积为126m2的厂房,工程条件是:
(1) 建1m新墙的费用为a元;(2) 修1m旧墙的费用为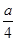 元;(3) 拆去1m的旧墙,用可得的建材建1m的新墙的费用为
元;(3) 拆去1m的旧墙,用可得的建材建1m的新墙的费用为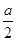 元,经讨论有两种方案:
元,经讨论有两种方案:
①利用旧墙一段x m(0<x<14)为矩形一边;
②矩形厂房利用旧墙的一面边长x≥14,问如何利用旧墙建墙费用最省?
试比较①②两种方案哪个更好。