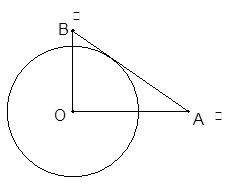设有半径为3 的圆形村落,
的圆形村落,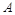 、
、 两人同时从村落中心出发。
两人同时从村落中心出发。 一直向北直行;
一直向北直行;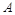 先向东直行,出村后一段时间,改变前进方向,沿着与村落边界相切的直线朝
先向东直行,出村后一段时间,改变前进方向,沿着与村落边界相切的直线朝 所在的方向前进。
所在的方向前进。
(1)若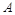 在距离中心5
在距离中心5 的地方改变方向,建立适当坐标系,
的地方改变方向,建立适当坐标系,
求: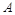 改变方向后前进路径所在直线的方程
改变方向后前进路径所在直线的方程
(2)设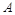 、
、 两人速度一定,其速度比为
两人速度一定,其速度比为 ,且后来
,且后来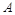 恰与
恰与 相遇.问两人在何处相遇?
相遇.问两人在何处相遇?
(以村落中心为参照,说明方位和距离)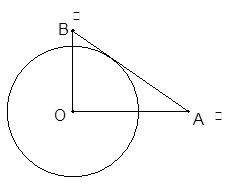
相关知识点
推荐套卷
设有半径为3 的圆形村落,
的圆形村落,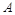 、
、 两人同时从村落中心出发。
两人同时从村落中心出发。 一直向北直行;
一直向北直行;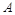 先向东直行,出村后一段时间,改变前进方向,沿着与村落边界相切的直线朝
先向东直行,出村后一段时间,改变前进方向,沿着与村落边界相切的直线朝 所在的方向前进。
所在的方向前进。
(1)若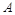 在距离中心5
在距离中心5 的地方改变方向,建立适当坐标系,
的地方改变方向,建立适当坐标系,
求: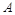 改变方向后前进路径所在直线的方程
改变方向后前进路径所在直线的方程
(2)设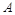 、
、 两人速度一定,其速度比为
两人速度一定,其速度比为 ,且后来
,且后来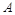 恰与
恰与 相遇.问两人在何处相遇?
相遇.问两人在何处相遇?
(以村落中心为参照,说明方位和距离)