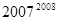你能比较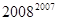 与
与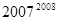 的大小吗?
的大小吗?
为了解决这个问题,我们首先写出它的一般形式,即比较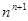 与
与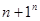 的大小(n是正整数),然后我们从分析n=1,n=2,n=3……中发现规律,经归纳、猜想得出结论
的大小(n是正整数),然后我们从分析n=1,n=2,n=3……中发现规律,经归纳、猜想得出结论
(1)通过计算,比较下列各组中两数的大小:(在横线上填写“>”“=”“<”)
①12 21,②23 32;③34 43;④45 54;⑤56 65
(2)从第(1)题的结果中,经过归纳,可以猜想出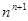 与(n+1)n的大小关系是
与(n+1)n的大小关系是
(3)根据以上归纳.猜想得到的一般结论,试比较下列两数的大小: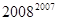 与
与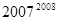
你能比较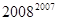 与
与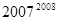 的大小吗?
的大小吗?
为了解决这个问题,我们首先写出它的一般形式,即比较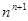 与
与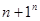 的大小(n是正整数),然后我们从分析n=1,n=2,n=3……中发现规律,经归纳、猜想得出结论
的大小(n是正整数),然后我们从分析n=1,n=2,n=3……中发现规律,经归纳、猜想得出结论
(1)通过计算,比较下列各组中两数的大小:(在横线上填写“>”“=”“<”)
①12 21,②23 32;③34 43;④45 54;⑤56 65
(2)从第(1)题的结果中,经过归纳,可以猜想出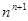 与(n+1)n的大小关系是
与(n+1)n的大小关系是
(3)根据以上归纳.猜想得到的一般结论,试比较下列两数的大小: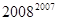 与
与