如图，B、C、E三点在一条直线上，⊿ABC和⊿DCE都为等边三角形，连接AE、DB、
（1）试说出 AE=BD的理由、
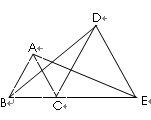
（2）如果把⊿DCE绕C点顺时针旋转一个角度，使B、C、E不在一条直线上,（1)中的结论还成立吗？（只回答，不说理由）
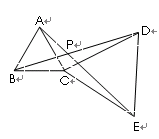
（3）在（2）中若AE、BD相交于P, 求∠APB的度数、
相关试题
与
－2成反比例，且当
时，求
（2）
的顶点为H，与
轴交于A、B两点（B点在A点右侧），点H、B关于直线：
对称，过点B作直线BK∥AH交直线于K点．
相关知识点
推荐套卷
如图，B、C、E三点在一条直线上，⊿ABC和⊿DCE都为等边三角形，连接AE、DB、
（1）试说出 AE=BD的理由、
（2）如果把⊿DCE绕C点顺时针旋转一个角度，使B、C、E不在一条直线上,（1)中的结论还成立吗？（只回答，不说理由）
（3）在（2）中若AE、BD相交于P, 求∠APB的度数、
粤公网安备 44130202000953号