如图1,正方形ABCD与正方形AEFG的边AB、AE(AB<AE)在一条直线上,正方形AEFG以点A为旋转中心逆时针旋转,设旋转角为 . 在旋转过程中,两个正方形只有点A重合,其它顶点均不重合,连接BE、DG.
. 在旋转过程中,两个正方形只有点A重合,其它顶点均不重合,连接BE、DG.
(1)当正方形AEFG旋转至如图2所示的位置时,求证:BE=DG;
(2)当点C在直线BE上时,连接FC,直接写出∠FCD 的度数;
(3)如图3,如果 =45°,AB =2,AE=
=45°,AB =2,AE=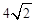 ,求点G到BE的距离.
,求点G到BE的距离.
相关知识点
推荐套卷
如图1,正方形ABCD与正方形AEFG的边AB、AE(AB<AE)在一条直线上,正方形AEFG以点A为旋转中心逆时针旋转,设旋转角为 . 在旋转过程中,两个正方形只有点A重合,其它顶点均不重合,连接BE、DG.
. 在旋转过程中,两个正方形只有点A重合,其它顶点均不重合,连接BE、DG.
(1)当正方形AEFG旋转至如图2所示的位置时,求证:BE=DG;
(2)当点C在直线BE上时,连接FC,直接写出∠FCD 的度数;
(3)如图3,如果 =45°,AB =2,AE=
=45°,AB =2,AE=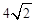 ,求点G到BE的距离.
,求点G到BE的距离.