(本小题满分13分)
已知函数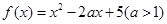 .
.
(1) 若函数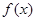 的定义域和值域均为
的定义域和值域均为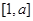 ,求实数
,求实数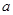 的值;
的值;
(2) 若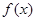 在区间
在区间 上是减函数,且对任意的
上是减函数,且对任意的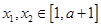 ,
,
总有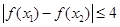 ,求实数
,求实数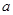 的取值范围;
的取值范围;
(3) 若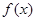 在
在 上有零点,求实数
上有零点,求实数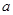 的取值范围.
的取值范围.
相关知识点
推荐套卷
(本小题满分13分)
已知函数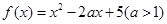 .
.
(1) 若函数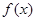 的定义域和值域均为
的定义域和值域均为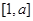 ,求实数
,求实数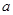 的值;
的值;
(2) 若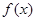 在区间
在区间 上是减函数,且对任意的
上是减函数,且对任意的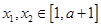 ,
,
总有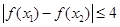 ,求实数
,求实数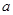 的取值范围;
的取值范围;
(3) 若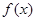 在
在 上有零点,求实数
上有零点,求实数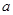 的取值范围.
的取值范围.