每年的农历三月初一为通州风筝节.这天,小刘同学正在江海明珠广场上放风筝,如图风筝从A处起飞,几分钟后便飞达C处,此时,在AQ延长线上B处的小宋同学,发现自己的位置与风筝和广场边旗杆PQ的顶点P在同一直线上.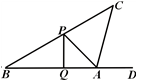
(1)已知旗杆高为10米,若在B处测得旗杆顶点P的仰角为30°,A处测得点P的仰角为45°,试求A、B之间的距离;
(2)此时,在A处背向旗杆又测得风筝的仰角为75°,若绳子在空中视为一条线段,求绳子AC为多少米?(结果可保留根号)
相关知识点
推荐套卷
 -
- =1.
=1.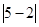 表示5与2差的绝对值,也可理解为5与2两数在数轴上所对应的两点之间的距离;
表示5与2差的绝对值,也可理解为5与2两数在数轴上所对应的两点之间的距离; 可以看做
可以看做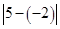 ,表示5与-2的差的绝对值,也可理解为5与-2两数在数轴上所对应的两点之间的距离.
,表示5与-2的差的绝对值,也可理解为5与-2两数在数轴上所对应的两点之间的距离.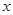 ,使
,使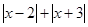 是否有最小值? 如果有,写出最
是否有最小值? 如果有,写出最 

 粤公网安备 44130202000953号
粤公网安备 44130202000953号