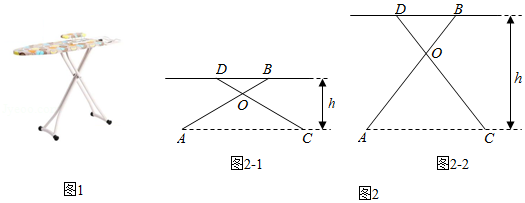
有一种升降熨烫台如图1所示,其原理是通过改变两根支撑杆夹角的度数来调整熨烫台的高度.图2是这种升降熨烫台的平面示意图. 和 是两根相同长度的活动支撑杆,点 是它们的连接点, , 表示熨烫台的高度.
(1)如图 .若 , ,求 的值;
(2)爱动脑筋的小明发现,当家里这种升降熨烫台的高度为 时,两根支撑杆的夹角 是 (如图 .求该熨烫台支撑杆 的长度(结果精确到 .
(参考数据: , , ,
相关知识点
推荐套卷
有一种升降熨烫台如图1所示,其原理是通过改变两根支撑杆夹角的度数来调整熨烫台的高度.图2是这种升降熨烫台的平面示意图. 和 是两根相同长度的活动支撑杆,点 是它们的连接点, , 表示熨烫台的高度.
(1)如图 .若 , ,求 的值;
(2)爱动脑筋的小明发现,当家里这种升降熨烫台的高度为 时,两根支撑杆的夹角 是 (如图 .求该熨烫台支撑杆 的长度(结果精确到 .
(参考数据: , , ,
