一汽车厂生产
三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):
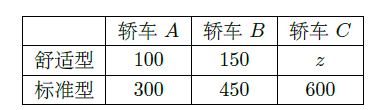
按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有
类轿车10辆.
⑴求
的值. 

⑵用分层抽样的方法在
类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
⑶用随机抽样的方法从
类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4, 8.6, 9.2, 9.6, 8.7, 9.3, 9.0, 8.2.把这8辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.