某企业决定用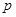
万元援助灾区
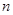所学校,用于搭建帐篷和添置教学设备。根据各校不同的受灾情况，该企业捐款的分配方案如下：所有学校得到的捐款数都相等，到第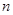所学校的捐款恰好分完，捐款的分配方法如下表所示. (其中,,
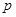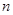都是正整数)
根据以上信息，解答下列问题：
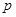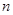(1)写出与的关系式；
(2)当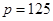
时，该企业能援助多少所学校？
(3)根据震区灾情，该企业计划再次提供不超过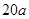
万元的捐款，按照原来的分配方案援助其它学校.若由 (2)确定,则再次提供的捐款最多又可以援助多少所学校？
相关试题
已知，如图，抛物线
与
轴交于点
，与
轴交于点
，点
的坐标为
，对称轴是
．
（1）求该抛物线的解析式；
（2）点
是线段
上的动点，过点作
∥
，分别交轴、
于点P、
，连接
．当
的面积最大时，求点的坐标；
（3）在（2）的条件下，求
的值.
已知：如图，
内接于⊙O, 
为⊙O的直径，
, 点
是
上一个动点，连结
、
和
, 与
相交于点
, 过点
作
于,
与相交于点
,连结
和
.
(1)求证：
;
（2）如图1，若
， 求证：
；
（3) 如图2，设
, 四边形
的面积为
,求与
之间的关系式.
，
，点P是AD边上一个动点，
, 
交
于点
，对应点
．
是等腰三角形，求
的长；
时，求
的长．
为迎接中共十八大的胜利召开，需要铺设一条长为3000米的管道．为了尽量减少施工对交通所造成的影响，实际施工时每天铺设管道的长度为原计划的1.5倍，结果提前25天完成任务，
（1）求原计划每天铺设管道的长度．
（2）求实际施工时每天铺设管道的长度．
、
。
；
相关知识点
推荐套卷
粤公网安备 44130202000953号