某运输公司接受了向抗洪救灾地区每天送至少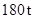 支援物资的任务.该公司有
支援物资的任务.该公司有 辆载重
辆载重 的
的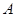 型卡车与
型卡车与 辆载重为
辆载重为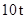 的
的 型卡车,有
型卡车,有 名驾驶员,每辆卡车每天往返的次数为
名驾驶员,每辆卡车每天往返的次数为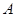 型卡车
型卡车 次,
次, 型卡车
型卡车 次;每辆卡车每天往返的成本费
次;每辆卡车每天往返的成本费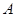 型为
型为 元,
元, 型为
型为 元.请为公司安排一下,应如何调配车辆,才能使公司所花的成本费最低?若只安排
元.请为公司安排一下,应如何调配车辆,才能使公司所花的成本费最低?若只安排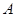 型或
型或 型卡车,所花的成本费分别是多少?
型卡车,所花的成本费分别是多少?
推荐套卷
某运输公司接受了向抗洪救灾地区每天送至少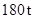 支援物资的任务.该公司有
支援物资的任务.该公司有 辆载重
辆载重 的
的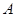 型卡车与
型卡车与 辆载重为
辆载重为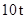 的
的 型卡车,有
型卡车,有 名驾驶员,每辆卡车每天往返的次数为
名驾驶员,每辆卡车每天往返的次数为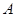 型卡车
型卡车 次,
次, 型卡车
型卡车 次;每辆卡车每天往返的成本费
次;每辆卡车每天往返的成本费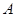 型为
型为 元,
元, 型为
型为 元.请为公司安排一下,应如何调配车辆,才能使公司所花的成本费最低?若只安排
元.请为公司安排一下,应如何调配车辆,才能使公司所花的成本费最低?若只安排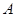 型或
型或 型卡车,所花的成本费分别是多少?
型卡车,所花的成本费分别是多少?