将一张透明的平行四边形胶片沿对角线剪开,得到图①中的两张三角形胶片 和
和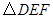 .将这两张三角形胶片的顶点
.将这两张三角形胶片的顶点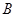 与顶点
与顶点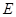 重合,把
重合,把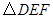 绕点
绕点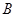 顺时针方向旋转,这时
顺时针方向旋转,这时 与
与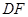 相交于点
相交于点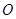 .
.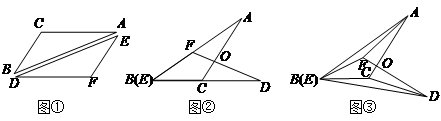
(1)当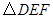 旋转至如图②位置,点
旋转至如图②位置,点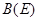 ,
,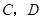 在同一直线上时,
在同一直线上时,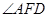 与
与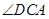 的数量关系是 . 2分
的数量关系是 . 2分
(2)当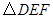 继续旋转至如图③位置时,(1)中的结论还成立吗?请说明理由.
继续旋转至如图③位置时,(1)中的结论还成立吗?请说明理由.
(3)在图③中,连接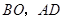 ,探索
,探索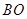 与
与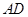 之间有怎样的位置关系,并证明.
之间有怎样的位置关系,并证明.
将一张透明的平行四边形胶片沿对角线剪开,得到图①中的两张三角形胶片 和
和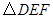 .将这两张三角形胶片的顶点
.将这两张三角形胶片的顶点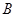 与顶点
与顶点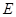 重合,把
重合,把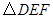 绕点
绕点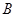 顺时针方向旋转,这时
顺时针方向旋转,这时 与
与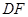 相交于点
相交于点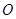 .
.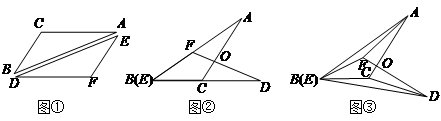
(1)当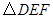 旋转至如图②位置,点
旋转至如图②位置,点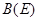 ,
, 在同一直线上时,
在同一直线上时,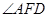 与
与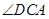 的数量关系是 . 2分
的数量关系是 . 2分
(2)当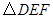 继续旋转至如图③位置时,(1)中的结论还成立吗?请说明理由.
继续旋转至如图③位置时,(1)中的结论还成立吗?请说明理由.
(3)在图③中,连接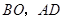 ,探索
,探索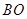 与
与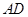 之间有怎样的位置关系,并证明.
之间有怎样的位置关系,并证明.