（本小题满分10分）我们用[a]表示不大于a的最大整数，例如：[2.5]=2，[3]=3，[﹣2.5]=﹣3；用＜a＞表示大于a的最小整数，例如：＜2.5＞=3，＜4＞=5，＜﹣1.5＞=﹣1．解决下列问题：
（1）[﹣4.5]= _________ ，＜3.5＞= _________ ．
（2）若[x]=2，则x的取值范围是 _________ ；若＜y＞=﹣1，则y的取值范围是 _____ ．
（3）已知x，y满足方程组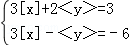
，求x，y的取值范围．
相关试题
（1）在下列横线上用含有a，b的代数式表示相应图形的面积.
① ②③④
（2）通过拼图，你发现前三个图形的面积与第四个图形面积之间有什么关系？请用数学式子表示：；
（3）利用（2）的结论计算992＋198＋1的值.
、
，其中
，小马在计算
时，由于粗心把
求得结果为
，请你帮小马算出
、
、
在数轴上的位置如图,化简：|c－b|＋|a＋b|－|a－c|.
，其中
．相关知识点
推荐套卷
粤公网安备 44130202000953号