在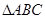 中,AC=25,AB=35,
中,AC=25,AB=35,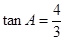 ,点D为边AC上一点,且AD=5,点E、F分别为边AB上的动点(点F在点E的左边),且∠EDF=∠A.设AE=x,AF=y.
,点D为边AC上一点,且AD=5,点E、F分别为边AB上的动点(点F在点E的左边),且∠EDF=∠A.设AE=x,AF=y.
(1)如图1,当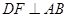 时,求AE的长;
时,求AE的长;
(2)如图2,当点E、F在边AB上时,求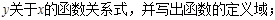
(3)联结CE,当 求
求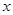 的值.
的值.
相关知识点
推荐套卷
在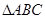 中,AC=25,AB=35,
中,AC=25,AB=35,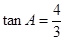 ,点D为边AC上一点,且AD=5,点E、F分别为边AB上的动点(点F在点E的左边),且∠EDF=∠A.设AE=x,AF=y.
,点D为边AC上一点,且AD=5,点E、F分别为边AB上的动点(点F在点E的左边),且∠EDF=∠A.设AE=x,AF=y.
(1)如图1,当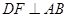 时,求AE的长;
时,求AE的长;
(2)如图2,当点E、F在边AB上时,求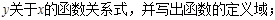
(3)联结CE,当 求
求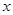 的值.
的值.