(本小题满分14分)
已知函数 ,
, ,
,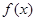 图象与
图象与 轴异于原点的交点M处的切线为
轴异于原点的交点M处的切线为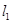 ,
, 与
与 轴的交点N处的切线为
轴的交点N处的切线为 , 并且
, 并且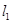 与
与 平行.
平行.
(1)求 的值;
的值;
(2)已知实数t∈R,求函数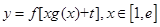 的最小值;
的最小值;
(3)令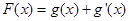 ,给定
,给定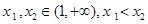 ,对于两个大于1的正数
,对于两个大于1的正数 ,
,
存在实数 满足:
满足: ,
,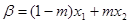 ,并且使得不等式
,并且使得不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
推荐套卷
(本小题满分14分)
已知函数 ,
, ,
,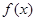 图象与
图象与 轴异于原点的交点M处的切线为
轴异于原点的交点M处的切线为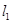 ,
, 与
与 轴的交点N处的切线为
轴的交点N处的切线为 , 并且
, 并且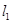 与
与 平行.
平行.
(1)求 的值;
的值;
(2)已知实数t∈R,求函数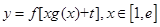 的最小值;
的最小值;
(3)令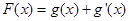 ,给定
,给定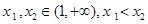 ,对于两个大于1的正数
,对于两个大于1的正数 ,
,
存在实数 满足:
满足: ,
,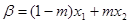 ,并且使得不等式
,并且使得不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.