阅读下面的情境对话,然后解答问题
(1)根据“奇异三角形”的定义,请你判断小华提出的命题:“等边三角形一定是奇异三角形”是真命题还是假命题?
(2)在Rt ABC 中, ∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt
ABC 中, ∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt ABC是奇异三角形,求a:b:c;
ABC是奇异三角形,求a:b:c;
(3)如图,AB是⊙O的直径,C是上一点(不与点A、B重合),D是半圆的中点,CD在直径AB的两侧,若在⊙O内存在点E使得AE=AD,CB=CE.
1求证: ACE是奇异三角形;
ACE是奇异三角形;
2当 ACE是直角三角形时,求∠AOC的度数.
ACE是直角三角形时,求∠AOC的度数.
相关知识点
推荐套卷
 .
.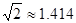 ,
,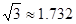 ,
, )
)
 ,BF=3,求⊙O的半径长.
,BF=3,求⊙O的半径长.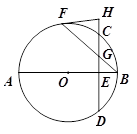
 粤公网安备 44130202000953号
粤公网安备 44130202000953号