(1)数轴上点A、点B分别是有理数-2、3对应的点,则点A、点B间的距离为 .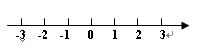
(2)再选几个点试试,猜想:若点A、点B分别是有理数a、b对应的点,则点A、点B间的距离为 .
(3)若数轴上点A对应的实数为a,且|a-2|=3,则点A对应的实数为 .
(4)若数轴上点A对应的实数为a,且|a-2|+|a+1|=5,则点A对应的实数为 .
相关知识点
推荐套卷
(1)数轴上点A、点B分别是有理数-2、3对应的点,则点A、点B间的距离为 .
(2)再选几个点试试,猜想:若点A、点B分别是有理数a、b对应的点,则点A、点B间的距离为 .
(3)若数轴上点A对应的实数为a,且|a-2|=3,则点A对应的实数为 .
(4)若数轴上点A对应的实数为a,且|a-2|+|a+1|=5,则点A对应的实数为 .