某学校办公楼前有一长为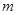
，宽为
的长方形空地，在中心位置留出一个半径为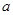
的圆形区域建一个喷泉，两边是两块长方形的休息区，阴影部分为绿地.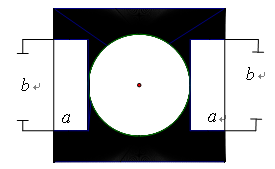
（1）用含字母和
的式子表示阴影部分的面积；
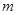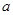（2）当=4，=3，=1，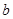
=2时，阴影部分面积是多少？（取3）
相关试题
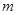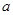某学校办公楼前有一长为，宽为的长方形空地，在中心位置留出一个半径为的圆形区域建一个喷泉，两边是两块长方形的休息区，阴影部分为绿地.
（1）用含字母和的式子表示阴影部分的面积；
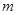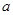（2）当=4，=3，=1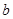，=2时，阴影部分面积是多少？（取3）
米，坡角(即∠BAC)为45°，BC⊥AC，现计划在斜坡中点D处挖去部分斜坡，修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE(下面两个小题结果都保留根号)．
，求休闲平台DE的长．
粤公网安备 44130202000953号