(本小题满分12分)已知函数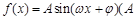 >0,
>0, >0,
>0,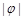 <
<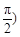 的图象与
的图象与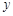 轴的交点为(0,1),它在
轴的交点为(0,1),它在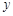 轴右侧的第一个最高点和第一个最低点的坐标分别为
轴右侧的第一个最高点和第一个最低点的坐标分别为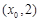 和
和
(1)写出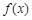 的解析式及
的解析式及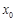 的值;
的值;
(2)若锐角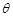 满足
满足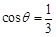 ,求
,求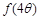 的值.
的值.
相关知识点
推荐套卷
(本小题满分12分)已知函数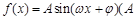 >0,
>0, >0,
>0,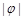 <
<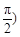 的图象与
的图象与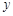 轴的交点为(0,1),它在
轴的交点为(0,1),它在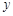 轴右侧的第一个最高点和第一个最低点的坐标分别为
轴右侧的第一个最高点和第一个最低点的坐标分别为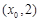 和
和
(1)写出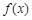 的解析式及
的解析式及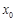 的值;
的值;
(2)若锐角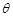 满足
满足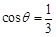 ,求
,求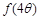 的值.
的值.