(1)观察图中的各个角，寻找对顶角(不含平角)：
①如图a中，共有_________对对顶角；
②如图b中，共有_________对对顶角；
③如图c中，共有_________对对顶角；
④探究①—③各题中直线条数与对顶角对数之间的关系，若有n条直线相交于一点，则可形成_________对对顶角；
(2)若n条直线两两相交于不同的点时，可形成_________对对顶角.你能将上述两种情形归纳一下吗?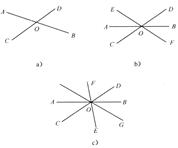
(1)观察图中的各个角，寻找对顶角(不含平角)：
①如图a中，共有_________对对顶角；
②如图b中，共有_________对对顶角；
③如图c中，共有_________对对顶角；
④探究①—③各题中直线条数与对顶角对数之间的关系，若有n条直线相交于一点，则可形成_________对对顶角；
(2)若n条直线两两相交于不同的点时，可形成_________对对顶角.你能将上述两种情形归纳一下吗?
(2)
(2)
粤公网安备 44130202000953号