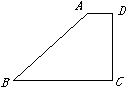
在直角梯形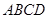 中,
中,  , 高
, 高 (如图1). 动点
(如图1). 动点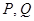 同时从点
同时从点 出发, 点
出发, 点 沿
沿 运动到点
运动到点 停止, 点
停止, 点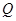 沿
沿 运动到点
运动到点 停止,两点运动时的速度都是1cm/s,而当点
停止,两点运动时的速度都是1cm/s,而当点 到达点
到达点 时,点
时,点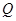 正好到达点
正好到达点 . 设
. 设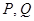 同时从点
同时从点 出发,经过的时间为
出发,经过的时间为 (s)时,
(s)时,  的面积为
的面积为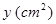 (如图2). 分别以
(如图2). 分别以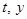 为横、纵坐标建立直角坐标系, 已知点
为横、纵坐标建立直角坐标系, 已知点 在
在 边上从
边上从 到
到 运动时,
运动时, 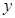 与
与 的函数图象是图3中的线段
的函数图象是图3中的线段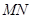 .
.


(图1) (图2)(图3)
(1)分别求出梯形中 的长度;
的长度;
(2)分别写出点 在
在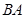 边上和
边上和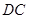 边上运动时,
边上运动时, 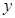 与
与 的函数关系式(注明自变量的取值范围), 并在图3中补全整个运动中
的函数关系式(注明自变量的取值范围), 并在图3中补全整个运动中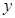 关于
关于 的函数关系的大致图象.
的函数关系的大致图象.
(3)问:是否存在这样的t,使PQ将梯形ABCD的面积恰好分成1:6的两部分?若存在,求出这样的t的值;若不存在,请说明理由.