如图，在△ABC中，∠C=90°，BC=5米，AC=12米．M点在线段CA上，从C向A运动，速度为1米/秒；同时N点在线段AB上，从A向B运动，速度为2米/秒．运动时间为t秒．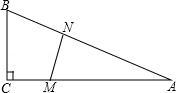
（1）当t为何值时，∠AMN=∠ANM？
（2）当t为何值时，△AMN的面积最大？并求出这个最大值．
相关试题
的和等于﹣1？
﹣（
﹣
）相关知识点
推荐套卷
如图，在△ABC中，∠C=90°，BC=5米，AC=12米．M点在线段CA上，从C向A运动，速度为1米/秒；同时N点在线段AB上，从A向B运动，速度为2米/秒．运动时间为t秒．
（1）当t为何值时，∠AMN=∠ANM？
（2）当t为何值时，△AMN的面积最大？并求出这个最大值．
粤公网安备 44130202000953号